Do rozwiązania zadań, związanych z określeniem powierzchni prostopadłościanu, należy jasno zrozumieć, co to jest ta geometryczna ciało, jakimi figurami są jego boczne ściany i podłoże. Poradzić sobie z rozwiązaniem pomoże znajomość właściwości danych geometrycznych kształtów.
Instrukcja
1
Параллепипед – to pryzmat, na podstawie której leży równoległobok. Параллелограммом nazywa się czworokąt, naprzeciwległe, którego boki są równe i równoległe. Prostopadłościan ma sześć ścian – górna i dolna podstawa i 4 bocznych krawędzi. Wszystkie one są параллелограммами. Ponieważ w warunku nie określa się kąt nachylenia bocznych ścian do podłoża, można uznać, że pryzmat jest bezpośredni. Stąd należy wyjaśnienie: u bezpośredni pryzmat boczne ściany – prostokąty.
2
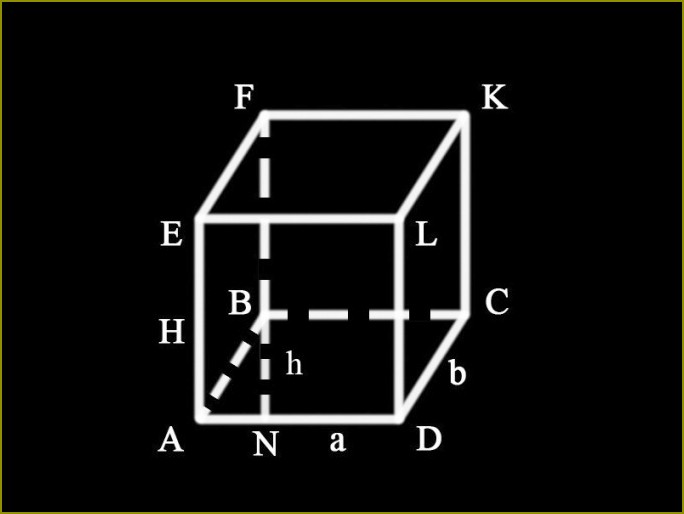
Aby znaleźć pole powierzchni prostopadłościanu, trzeba znaleźć jego powierzchnia podstawy i powierzchni bocznej powierzchni. Aby to zrobić, należy znać długość boków podstawy prostopadłościanu i długość jego żebra. Dla określania powierzchni podłoża należy przeprowadzić wysokość równoległoboku. Można uznać, że wartości te są znane, ponieważ warunkiem, że ten element nie jest do uzgodnienia. Dla ułatwienia wprowadzone oznaczenia:AD = BC = a – podstawy równoległoboku;AB = CD = b – boki równoległoboku;BN = h – wysokość równoległoboku;AE = DL = CK = BF = H – krawędź prostopadłościanu.
3
Powierzchnia równoległoboku jest określana jako iloczyn jego podstawy na wysokości, tj. ah. Ponieważ górne i dolne podstawy są równe, ich łączna powierzchnia S = 2ah.
4
Ponieważ boczne ściany są prostokątami, a ich powierzchnia jest obliczana jako iloczyn stron. Jedna strona ściany AELD jest na krawędzi prostopadłościanu i równa H, a drugą stroną jego podstawy i równa a. Powierzchnia ściany: aH. Boczne ściany prostopadłościanu są parami równe i równoległe. Ściana AELD równa ściany BFKC. Ich łączna powierzchnia S = 2aH.
5
Ściana AEFB równa ściany DLKC. Strona AB pokrywa się z boku podstawy prostopadłościanu i równa się b, strona AE jest równa H. Powierzchnia ściany AEFB równa bH. Suma pól powierzchni tych ścian S = 2bH. Powierzchnia boczna prostopadłościanu: 2aH+2bH.
6
W ten sposób, powierzchnia powierzchni prostopadłościanu: S = 2ah+2aH+2bH lub S = 2(ah+aH+bH)problem rozwiązany.

Kategoria:
Matematyka





