Ułamek składa się z licznika, znajdującego się na górze linii, i mianownika, na który jest podzielony, znajdującego się na dole. Irracjonalne nazywa się liczba, która nie może być przedstawiona w postaci ułamka z liczbą na liczniku i naturalnym w mianowniku. Takimi liczbami są, na przykład, pierwiastek kwadratowy z dwóch lub pi. Zwykle, gdy mówi się o irracjonalności w mianowniku oznacza korzeń.
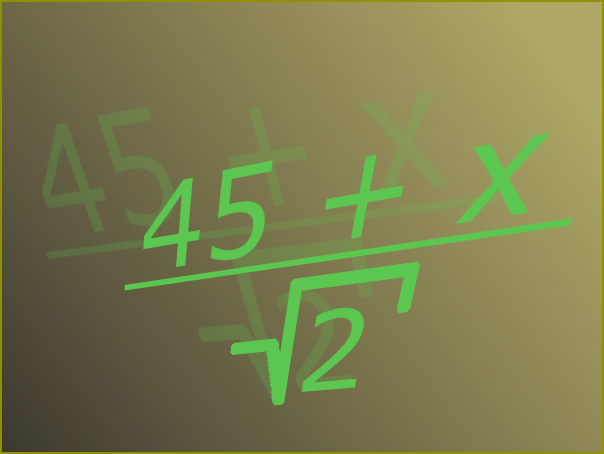
Instrukcja
1
Pozbądź się irracjonalności mnożeniem na mianownik. W ten sposób irracjonalność zostanie przeniesiona w liczniku. Po pomnożenie licznika i mianownika na jedno i to samo liczba, wartość ułamka się nie zmienia. Użyj tej opcji, jeśli cały mianownik jest korzeń.
2
Pomnóż licznik i mianownik na mianownik odpowiednią liczbę razy, w zależności od korzenia. Jeśli pierwiastek kwadratowy, to raz.
3
Rozważmy przykład z kwadratowym korzeniem. Weź śrut (56-y)/v(x+2). Jest w niej licznik (56-y) i irracjonalny mianownik v(x+2), czyli pierwiastek kwadratowy.
4
Pomnóż licznik i mianownik ułamka o mianowniku, czyli na v(x+2). Pierwszy przykład (56-y)/v(x+2) zamieni się w ((56-y)*v(x+2))/(v(x+2)*v(x+2)). W końcu się uda ((56-y)*v(x+2))/(x+2). Teraz korzeń znajduje się w liczniku, a w mianowniku nie irracjonalności.
5
Nie zawsze mianownik ułamka pełna jest pod korzeniem. Pozbądź się irracjonalności, korzystając z wzoru (x+y)*(x-y)=x?-y?.
6
Rozważmy przykład z frakcji (56-y)/(v(x+2)-vy). Jej irracjonalny mianownik zawiera różnicę dwóch metrów korzeni. Uzupełnij mianownik do formuły (x+y)*(x-y).
7
Pomnożyć mianownik na kwotę korzeni. Pomnóż na to samo licznik, aby wartość ułamka się nie zmieniło. Śrut zmieni ((56-y)*(v(x+2)+vy))/((v(x+2)-vy)*(v(x+2)+vy)).
8
Skorzystaj z wyżej wymienionych funkcji (x+y)*(x-y)=x?-y? i uwolnij mianownik od irracjonalności. W rezultacie uda ((56-y)*(v(x+2)+vy))/(x+2-y). Teraz korzeń znajduje się w liczniku, a w mianowniku pozbył się irracjonalności.
9
W trudnych przypadkach powtarzaj obie te opcje, stosując w razie potrzeby. Należy pamiętać, że nie zawsze jest to możliwe, aby pozbyć się irracjonalności w mianowniku.

Kategoria:
Matematyka





