Często wiadomo, że y zależy od x liniowo, i dany jest wykres tej zależności. W tym przypadku może dowiedzieć się równanie prostej. Najpierw trzeba wybrać się na prostej dwa punkty.

Instrukcja
1
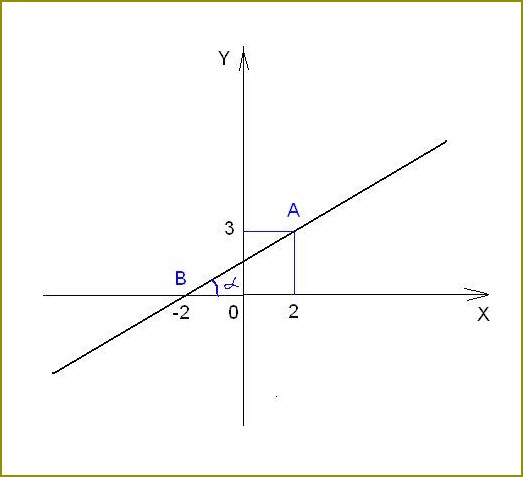
Na rysunku wybraliśmy punkty A i B. Wygodnie wybierać punkty przecięcia z osiami. Dwóch punktów wystarczy do tego, aby dokładnie określić bezpośrednie.
2
Znajdź współrzędne wybranych punktów. Opuść normalne punktów na osi współrzędnych i zapisać liczby z osi. Tak dla punktu B z naszego przykład współrzędna x jest równa -2, a współrzędna y – 0. Podobnie dla punktu A współrzędne będą (2;3).
3
Wiadomo, że równanie prostej ma postać y = kx + b. Zastąpić równanie w sumie jako współrzędne wybranych punktów, następnie do punktu A, to otrzymamy równanie: 3 = 2k +b. Do punktu B, otrzymujemy drugie równanie: 0 = -2k + b. Oczywiście, że mamy układ dwóch równań z dwiema niewiadomymi: k i b.
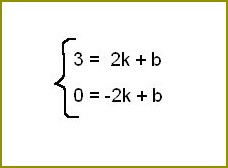
4
Dalej rozwiązujemy układ dowolny sposób. W naszym przypadku można złożyć układu równań, tak jak nieznany k wchodzi w oba równania o współczynnikach, które są takie same modulo, ale przeciwny znak. Wtedy otrzymamy 3 + 0 = 2k 2k + b + b, lub, co jest tym samym: 3 = 2b. W ten sposób b = 3/2. Zastąpić znajdująca wartość b w każdym z równań, aby znaleźć k. Wtedy 0 = -2k + 3/2, k = 3/4.
5
Zastąpić znalezione k i b do równania ogólnego wyglądu i otrzymamy szukane równanie prostej: y = 3x/4 + 3/2.
Należy zwrócić uwagę
Współczynnik k nazywa dziękujemy współczynnik prostej i wynosi тангенсу kąta między prostą a osią x.

Kategoria:
Matematyka





