Aby rozwiązać ten problem, należy pamiętać, że to jest ścięty i jakie właściwości posiada. Koniecznie zrób rysunek. To pozwoli określić, jaką figurę geometryczną stanowi przekrój stożka. Całkiem możliwe, że po tym, rozwiązanie zadania nie będzie już stanowić dla ciebie trudności.
Instrukcja
1
Okrągły stożek – ciało, otrzymanej przez obrót tego trójkąta wokół jednej z jego nóg. Proste, wychodzące z wierzchołka stożka i przekraczające jego podstawie, nazywane tworzą. Jeśli wszystkie generatory są równe, stożek jest bezpośrednim. W podstawie okrągłego stożka leży koło. Normalna, opuszczony na podstawie z góry, jest wysokość stożka. U okrągłego bezpośredniego wysokość stożka pokrywa się z jego osią. Oś jest prosta, łącząca wierzchołek ze środkiem podstawy. Jeśli pozioma секущая płaszczyznę okrągłego stożka jest równoległa do podłoża, jego górna podstawa jest koło.
2
Ponieważ w założeniu zadania nie podano, jaki stożek stosowany w tym przypadku, można stwierdzić, że jest to okrągły prosto ścięty, poziomy przekrój którego równolegle do podłoża. Jego przekrój osiowy, czyli pionowe płaszczyzny, która przechodzi przez oś okrągłego ściętego stożka, jest равнобочную trapez. Wszystkie osiowe przekroju okrągłego bezpośredniego stożka jest równe między sobą. Dlatego też, aby znaleźć powierzchnia przekroju osiowego, chcesz znaleźć powierzchnia trapezu, zasadami, które są średnice podstaw ściętego stożka, a na boki – go tworzące. Wysokość ściętego stożka jest jednocześnie wysokością trapezu.
3
Powierzchnia trapezu jest ustalana według wzoru:S = ?(a+b) h, gdzie S – powierzchnia trapezu;a – wartość dolnej podstawy trapezu;b – wartość jej górnej podstawy;h – wysokość trapezu.
4
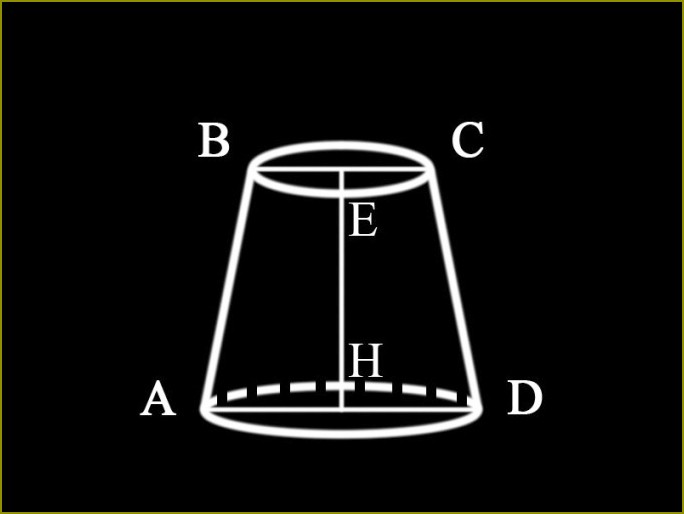
Ponieważ warunkiem nie inaczej, jakie wartości są podane, można uznać, że średnice obu podstaw i wysokości ściętego stożka znane: AD = d1 – średnica dolnej podstawy ściętego stożka;BC = d2 – średnica jego górnej podstawy; EH = h1 – wysokość stożka.W ten sposób powierzchnia przekroju osiowego ściętego stożka określa: S1 = ? (d1+d2) h1

Kategoria:
Matematyka





