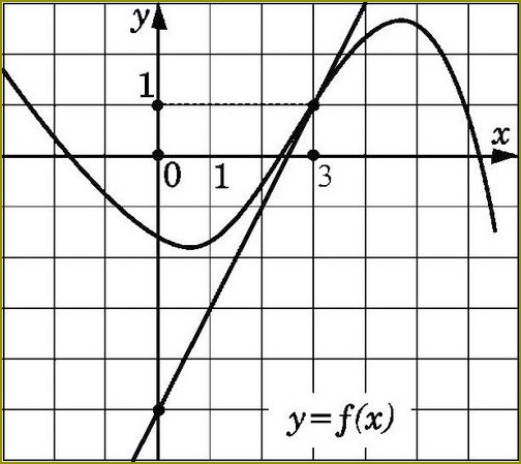
Prosta y = f(x) będzie być styczna do wykresu, przedstawiono na rysunku w punkcie x0, pod warunkiem, jeśli przechodzi przez dany punkt o współrzędnych (x0; f(x0)) i ma nachylenie f'(x0). Znaleźć współczynnik ten, biorąc pod uwagę cechy styczna, proste.
Trzeba
- – matematyczny kieszonkowy;
- – terminarz;
- – prosty ołówek;
- – klamka;
- – kątomierz;
- – cyrkiel.
Instrukcja
1
Należy pamiętać, że harmonogram дифференцируемой funkcji f(x) w punkcie x0 nie ma różnic z odcinkiem styczności. W związku z tym jest dość zbliżony do odcinka l, do przechodzącego przez punkty (x0; f(x0)) i (x0+?x; f(x0 + ?x)). Aby ustawić prostą, przechodzącą przez punkt A z współczynnikami (x0; f(x0)), wprowadź jej nachylenie. Przy tym jest on równy ?y/?x wskazującą styczna (?x>0) , a także dąży do liczby f'(x0).
2
Jeśli wartości f'(x0) nie istnieje, to może styczności nie, lub przechodzi pionowo. W związku z tym, obecność pochodnej funkcji w punkcie x0 wynika istnienie невертикальной styczna, która styka się z wykresu funkcji w punkcie (x0, f(x0)). W tym przypadku nachylenie stycznej jest równa f'(x0). Staje się jasne geometryczny sens pochodnej, czyli obliczanie współczynnika kątowego styczna.
3
Czyli aby znaleźć nachylenie stycznej, trzeba znaleźć wartość pochodnej funkcji w punkcie styczności. Przykład: znaleźć nachylenie stycznej do wykresu funkcji y = x? w punkcie абсциссой X0 = 1. Rozwiązanie: Znajdź pochodną tej funkcji?(x) = 3x?; znajdź wartość pochodnej w punkcie X0 = 1. u?(1) = 3 ? 1? = 3. Nachylenie stycznej w punkcie X0 = 1 jest równa 3.
4
Narysuj na rysunku aby uzyskać więcej styczne w taki sposób, aby stykały się z wykresem funkcji w następujących punktach: x1, x2 i x3. Zaznacz kąty, które tworzą się danymi styczne z osią x (kąt liczony w pozytywnym kierunku – od osi do prostej stycznej). Na przykład, pierwszy kąt ?1 będzie ostry, drugi (?2) – głupi, no a trzeci (?3) będzie równa zeru, ponieważ przeprowadzona prosta styczna jest równoległa do osi OX. W tym przypadku tangens jednego z kątów ma wartość ujemną, a tangens kąta ostrego – pozytywny, podczas tg0 i wynik jest równy zero.

Kategoria:
Matematyka





