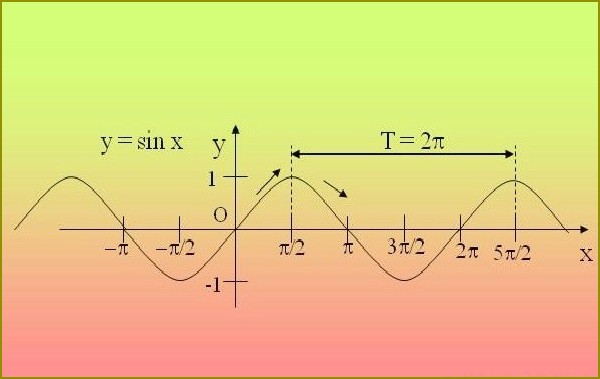
Funkcje trygonometryczne периодичны, czyli powtarza się przez pewien okres. Dzięki temu wystarczy zbadać funkcji na tym przedziale i rozprzestrzeniać znalezione właściwości w pozostałych okresach.
Instrukcja
1
Jeśli wam dano proste wyrażenie, w którym występuje tylko jedna тригонометрическая funkcji (sin, cos, tg, ctg, sec, cosec), przy czym kąt wewnątrz funkcji nie pomnożone przez jakąś liczbę, a ona sama nie wzniesiona w jakikolwiek stopień – skorzystaj z definicją. Dla wyrażeń zawierających sin, cos, sec, cosec śmiało umieszczać okresie 2N, a jeśli w równaniu jest tg, ctg – to P. na Przykład, dla funkcji y=2 ѕіпх+5 okres będzie równy 2N.
2
Jeśli kąt x pod znakiem тригонометрической funkcji pomnożone przez jakąś liczbę, to, aby znaleźć okres tej funkcji, należy podzielić standardowy okres na to liczba. Na przykład, dana jest funkcja y= sin 5x. Standardowy okres sinus – 2P, dzieląc go na 5, dostaniesz 2N/5 – to jest szukany okres tego wyrażenia.
3
Aby znaleźć okresie тригонометрической funkcji, wzniesionej w stopień ocenić parzystość stopniu. Dla parzystego stopnia zmniejszyć standardowy okres dwa razy. Na przykład, jeśli dana jest funkcja y=3 cos^2x, standardowy okres 2N zmniejszy się 2 razy, więc okres będzie równy P. Należy zwrócić uwagę, że funkcje tg, ctg w jakimkolwiek stopniu периодичны P.
4
Jeśli wam dane jest równanie, które zawiera iloczyn lub iloraz dwóch funkcji trygonometrycznych, najpierw znajdź okres dla każdej z nich oddzielnie. Następnie znajdź minimalna liczba, która умещало w sobie całkowitą ilość obu okresów. Na przykład, dana jest funkcja y=tgx*cos5x. Dla tangens okresie N, dla cosinus 5x – okres 2N/5. Minimalna liczba, w którym można zmieścić zarówno tych z okresu, to 2N, zatem szukany okres – 2P.
5
Jeśli nie wiesz, jak działać zaoferowanego sposób lub wątpliwości w odpowiedzi, spróbuj działać z definicji. Weź jako okresu funkcji T, jest większy od zera. Podstawiając do równania zamiast x wyrażenie (x+T) i zdecyduje się na otrzymaną równość, jak gdyby T parametrem lub liczbą. W wyniku znajdziesz wartość тригонометрической funkcji i można dobrać minimalny okres. Na przykład, w wyniku uproszczenia udało ci się tożsamość sin (T/2)=0. Minimalna wartość T, w którym ono działa, jest równa 2N, to i będzie to odpowiedź do zadania.

Kategoria:
Matematyka





