Zakrzywiony całka bierze się wzdłuż jakiejś płaskiej lub przestrzennej krzywej. Do obliczeń przyjęte formuły, które obowiązują przy spełnieniu określonych warunków.
Instrukcja
1
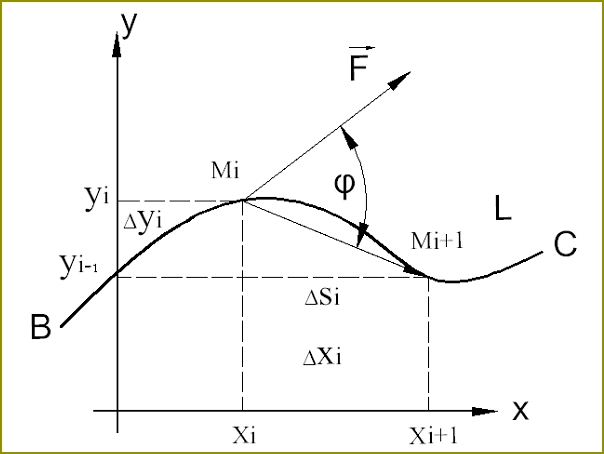
Niech na krzywej w układzie współrzędnych kartezjańskich określona jest funkcja F(x, y). Do całkowania funkcji krzywej jest podzielona na odcinki o długości zbliżonej do 0. Wewnątrz każdego takiego odcinka wybrane punkty Mi o współrzędnych xi, yi, określane są wartości funkcji w tych punktach F(Mi) i są mnożone na długości odcinków:F(M1)·?s1 + F(M2)·?s2 + … F(Mn)·?sn = ?F(Mi)·?si w 1 ? I ? n.
2
Uzyskana kwota nazywa zakrętach integralną kwoty. Odpowiednia całka jest równa granicy od tej kwoty:?F(x, y)ds = lim ?F(Mi)·?si = lim ?F(xi, yi)· v ((?xi)? + (?yi)?) = lim F(xi, yi)·v(1 + (?yi/?xi) ?)·?xi = ?F(x, y)·v(1 + (y’)?)dx.
3
Przykład.Znajdź zakrzywiony całka ?x?·yds wzdłuż linii y = ln x 1 ? x ? e.Rozwiązanie.Według wzoru:?x?yds = ?x?·v(1 + ((ln x)’)?) = ?x?·v(1 + 1/x?) = ?x? ·v((1 + x?)/x) = ?x·v(1 + x?)dx = 1/2·?v(1 + x?)d(1 + x?) = ?·(1 + x)^3/2 = [1 ? x ? e] = 1/3·((1 + e?)^3/2 – 2^3/2) ? 7,16.
4
Niech krzywa jest ustawiona w formie parametrycznej x = ?(t), y = ?(t). Aby obliczyć zakrzywiony całka, dotyczy już znaną formułę:?F(x, y)ds = lim ?F(Mi)·?si = lim ?F(xi, yi)·v((?xi)? + (?yi)?).
5
Po wprowadzeniu wartości x i y, otrzymamy:?F(x, y)ds = lim ? F(?(ti), ?(ti))·v(?? (ti) + ?? (ti))·?ti = ?F(?(t)?(t))·v(?? + ??)dt.
6
Przykład.Oblicz zakrzywiony całka ?y?ds, jeśli linia jest ustawiona parametrycznie: x = 5·cos t, y = 5·sin t 0 ? t ? ?/2.Rozwiązanie.ds = (25·cos? t + 25·sin? t)dt = 5dt.?y?ds = ?25·sin?t·5dt = 125/2?(1 – cos 2t)dt = 125/2·(t – sin 2t/2) = [0 ? t ? ?/2] = 125/2·((?/2 – 0) – (0 – 0)) = 125/2·?/2 = 125·?/4.

Kategoria:
Matematyka





