Pojęcie całki bezpośrednio związane z pojęciem całki z funkcji. Innymi słowy, aby znaleźć całki określonej funkcji, trzeba znaleźć taką funkcję, w stosunku do której pierwotna będzie pochodną.
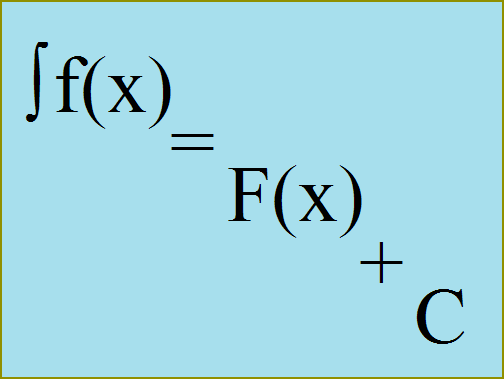
Instrukcja
1
Całka odnosi się do pojęć analizy matematycznej i graficznie jest powierzchnia zakrętach trapezu, ograniczonej oś x maksimum punktów całkowania. Znalezienie całki funkcji znacznie trudniejsze, niż szukać jej pochodną.
2
Istnieje kilka metod obliczania nieokreślony całki: bezpośrednie integracja, wprowadzenie pod znak mechanizmu różnicowego, metoda podstawiania, całkowanie przez części, rozwijanie Вейерштрасса, twierdzenie Newtona-Leibniza, itp.
3
Bezpośrednia integracja zakłada doprowadzenie za pomocą prostych przekształceń pierwotnego całki na stole wartości. Na przykład:?dy/(sin?y·cos?y) = ?(cos?y + sin?y)/(sin?y·cos?y)dy = ?dy/sin?y + ?dy/cos?y = -ctgy + tgy + C.
4
Metoda iniekcji pod znak mechanizmu różnicowego lub wymiana zmiennej jest postawienie nowej zmiennej. Przy tym oryginalny całka sprowadza się do nowego интегралу, który można przekształcić na stole rodzaju metodą bezpośredniego całkowania:Niech jest całka ?f(y)dy = F(y) + C i pewna zmienna v = g(y), wtedy:?f(y)dy -> ?f(v)dv = F(v) + C.
5
Należy pamiętać, niektóre pierwotniaki wyszukiwania dla ułatwienia pracy z tą metodą:dy = d(y + b);ydy = 1/2·d(y? + b);sinydy = – d(cosy);cosydy = d(sine wiry).
6
Przykład:?dy/(1 + 4·y?) = ?dy/(1 + (2·y) ?) = [dy -> d(2·y)] = 1/2·?d(2·y)/(1 + (2·y) ?) = 1/2·arctg2·y + C.
7
Całkowanie przez części odbywa się według następującego wzoru:?udv = u·v ?vdu.Przykład:?y·sinydy = [u = y; v = sine wiry] = y·(-cosy) – ?(-cosy)dy = -y·cosy + sine wiry + C.
8
Całkę w większości przypadków znajduje się na twierdzenia Newtona-Leibniza:?f(y)dy na przedziale [a; b] jest równa F(b) – F(a).Przykład: Znajdź ?y·sinydy na przedziale [0; 2?]:?y·sinydy = [u = y; v = sine wiry] = y·(-cosy) – ?(-cosy)dy = (-2?·cos2? + sin2?) – (-0·cos0 + sin0) = -2?.

Kategoria:
Matematyka





