Matryca jest uporządkowanym zbiorem liczb w prostokątnej tabeli, która ma wymiar m wierszy na n kolumn. Rozwiązanie skomplikowanych układów równań liniowych opiera się na obliczeniu macierzy, składających się z określonych współczynników. W ogólnym przypadku przy obliczaniu macierzy znajdują jej determinant. Wyznacznik (Det A) matrycy 5 kolejności wskazane jest uważać za pomocą rekurencyjnego obniżenia wymiaru metodą rozkładu w wierszu lub kolumnie.
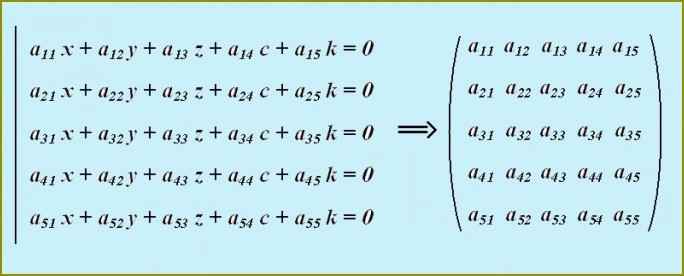
Instrukcja
1
Do obliczenia детерминанта (Det A) macierzy wymiaru 5×5 przesuń rozkład elementów na pierwszej linii. Do tego weź pierwszy element tego ciągu i wykreślić z macierzy wiersz i kolumnę, na przecięciu których znajduje się. Zapisz formułę dzieła pierwszego elementu i dostawca otrzymanej macierzy 4 zamówienia: a11*detM1 – to będzie pierwsza kadencja w celu znalezienia Det A. W pozostałej четырехразрядной macierzy M1 trzeba będzie później znaleźć wyznacznik (artykuł-moll).
2
W podobny sposób, konsekwentnie odpada kolumnę i wiersz, zawierające 2, 3, 4 i 5 element pierwszego wiersza początkowej macierzy, i znaleźć dla każdego z nich odpowiednią macierz 4×4. Zapisz dzieła tych elementów na dodatkowe миноры: a12*detM2, a13*detM3, a14*detM4, a15*detM5.
3
Znajdź determinanty otrzymanych macierzy 4 rzędu. Do tego przeciągnij ponownie tą samą metodą obniżenie wymiaru. Pierwszy element b11 macierzy M1 pomnożyć przez dostawcę pozostałej macierzy 3×3 (C1). Determinanty sam trójwymiarowej matrycy można łatwo obliczyć na podstawie wzoru: detC1 = c11* c22*c33 + c13* c21*c32 + c12* c23*c31 – c21* c12*c33 – c13* c22*c31 – c11* c32*c23, gdzie cij – elementy otrzymanej macierzy C1.
4
Dalej należy rozważyć analogicznie drugi element b12 macierzy M1 i oblicz jego dzieło z odpowiednim dodatkowym минором detC2 uzyskanych trójwymiarowej matrycy. W ten sam sposób znajdź utwory na 3 i 4 pozycji pierwszej macierzy 4 rzędu. Po czym określić szukany artykuł-moll matrycy detМ1. Do tego, według wzoru rozkładu w wierszu zapisz wyrażenie: detМ1 = b11*detC1 – b12*detC2 + b13*detC3 – b14*detC4. Masz pierwsza kadencja, wymagana w celu znalezienia Det A.
5
Oblicz pozostałe suma wyznacznika macierzy piątego rzędu, w podobny sposób obniża wymiar każdej macierzy 4 rzędu. Ostateczna formuła wygląda tak: Det A = a11*detM1 – a12*detM2 + a13*detM3 – a14*detM4 + a15*detM5.

Kategoria:
Matematyka





